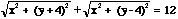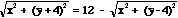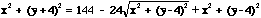
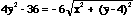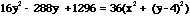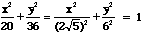Lesson 4

Now let us think about the definition of an ellipse a little more in-depth.

This definition makes note that the sum of two distances is a constant. This constant is refered to as k or the focal constant. One would think then that if we were given the coordinates of the foci for an ellipse and the focal constant, we could derive an equation for the ellipse. This is a correct assumption. In order to derive this equation, one needs to know the distance formula. The distance formula lets one find the distance between two points in the plane. If we are given the points (x,y) and (a,b), the distance between these two points is equal to the sqrt((x-a)² + (y-b)²). Therefore, if we are given that the focal constant is k and the foci are at the points (a,b) and (c,d), then the set of all points (x,y) that when you sum the distances from (a,b) to (x,y) and (c,d) to (x,y) that are equal to the focal constant k, is the locus of points of the ellipse with foci at (a,b) and (c,d) and a focal constant of k.

Example

How would you go about deriving the equation of the ellipse if all you were given was the coordinates of the foci and the focal constant?

1. Assume that we were given that the foci were located at (0,4) and (0,-4) and the focal constant was 12. We know that the focal constant is the sum of the distances from some point (x,y) to (0,4) and (x,y) to (0,-4). Therefore, we can set up an equation that resembles this and looks like.
2. Now subtracting the square root term that contains (y-4) from both sides we end up with .
3. If we square both sides, we have
4. Simplifying, we get.
5. Now squaring both sides again, we have.
6. Simplifying, we have 720 = 36x² + 20y².
7. Finally, dividing both sides by 720, we arrive at the equation in standard form.

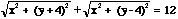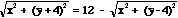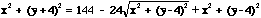
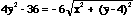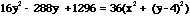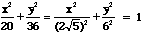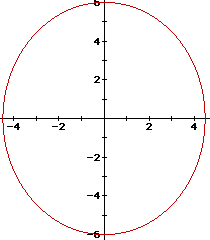
The graph of this equation would look like

Homework Assignment 4

Back to Ellipse Lesson