Lesson 3
Once again,
|
Definition of Ellipse |
An ellipse is the set of all points in the plane such that the sum
of the distances from two given points, called the foci, is a constant.
This constant is called the focal constant. |
What happens when the center of the ellipse is not located at the origin
but at some point (h,k)? How does the standard form of the equation
change to accommodate for the ellipse not being at the origin? If the center
of the ellipse is not at the origin, then it is shifted either in the x
direction, y direction or both. This shift gives us a new standard
form of the equation for an ellipse, which looks like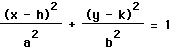 . From this, one will notice that if both h and k
are zero, the equation resembles the standard form of the equation when
the ellipse is centered at the origin. Thus, h and k not only
determine the center of the ellipse but the shift of the ellipse in the
x and y directions also, respectively. The graphs below illustrate
ellipses not centered at the origin but rather at some point (h,k).
. From this, one will notice that if both h and k
are zero, the equation resembles the standard form of the equation when
the ellipse is centered at the origin. Thus, h and k not only
determine the center of the ellipse but the shift of the ellipse in the
x and y directions also, respectively. The graphs below illustrate
ellipses not centered at the origin but rather at some point (h,k).
|
|
|
|
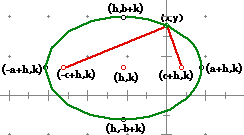
a > b |
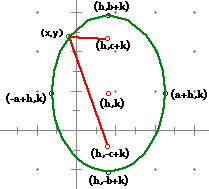
b > a |
The method for finding the foci of ellipses of this form is the same
as it was when the ellipse was centered at the origin other than you have
to take into account the shift. The two pictures above illustrate this point
quite well by showing that the foci are either (-c+h,k) and (c+h,k),
for a>b, or (h,c+k) and (h,-c+k), for b>a.
Example
When the ellipse is not centered at the origin, many times is more difficult
to get the equation that one is given into standard form. For example, to
put the equation 4x2 + y2
+ 16x - 2y = -1 into standard form, one needs to use the completing
the square method to do so. The method of completing the square is illustrated
below to refresh your memory on the concept. Once the equation is in standard
form, we will determine the coordinates of the vertices of the major and
minor axes and of the foci, and graph the ellipse.
- The first thing that one needs to do when completing the square is
to gather all terms containing an x together and all terms containing
a y together. So in our example, we have 4x2
+ 16x and y2 - 2y.
- Once this is done, in order to complete the square, the coefficient
on the squared term(s) has to be 1. The coefficient on the y2
term is already 1, so we do not have to do anything with that. However,
the coefficient of the x2 term is 4.
Therefore, we need to divide all the x terms by 4. We now
have 4(x2 + 4x) + y2
- 2y = -1.
- Now, to complete the square of the x terms in the parenthesis,
we need to take 1/2 of the coefficient of the x term and square
it. Thus, 1/2(4) = 2, and 22 = 4.
Now add this four to the expression inside the parenthesis. Since we just
added 4 inside the parenthesis, we need to account for it outside
of the parenthesis. Notice that the parenthesis are multiplied by 4,
thus we must subtract 16 from the left side of the equation to keep
the equation balanced. Our equation now looks like, 4(x2
+ 4x + 4) + y2 - 2y -16 = -1.
- Using the same logic just used in step 3, we take 1/2 of the coefficient
of the y term and square it. So, we end up with 1/2(-2) = -1,
-12 = 1. Therefore, we add one
to the y2 - 2y terms. By doing
this we must also subtract 1 from the rest of the left side of the
equation. Our equation now looks like, 4(x2
+ 4x + 4) + (y2 - 2y + 1) -17
= -1.
- Now, we can simplify the terms inside both sets of parenthesis to arrive
at an equation:
4(x + 2)2 + (y - 1)2
-17 = -1.
- We now add 17 to both sides give us, 4(x + 2)2
+ (y - 1)2 = 16.
- Now we can put this equation into standard form by dividing both sides
by 16 and simplifying.
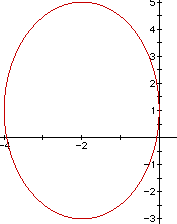
From this, we can see that the center of the ellipse is at (-2,1)
and that a = 2, b = 4 and c =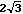 . If this ellipse was centered at the origin, the coordinates
of the vertices of the major and minor axes would be (0,-4), (0,4),
(-2,0) and (2,0), respectively, and of the foci would be
(0,-
. If this ellipse was centered at the origin, the coordinates
of the vertices of the major and minor axes would be (0,-4), (0,4),
(-2,0) and (2,0), respectively, and of the foci would be
(0,-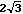 )
and (0,
)
and (0,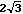 ). Since
this ellipse is not centered at the origin we need to shift each of the
coordinates just determine in the x and y directions by -2
and 1, respectively. So the actual coordinates of the vertices of
the major and minor axes other this ellipse are (-4,1), (0,1), (-2,-3),
and (-2,5) and of the foci would be (-2,1-
). Since
this ellipse is not centered at the origin we need to shift each of the
coordinates just determine in the x and y directions by -2
and 1, respectively. So the actual coordinates of the vertices of
the major and minor axes other this ellipse are (-4,1), (0,1), (-2,-3),
and (-2,5) and of the foci would be (-2,1-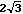 ) and (-2,1+
) and (-2,1+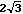 ). Now graphing this ellipse, one would
get
). Now graphing this ellipse, one would
get
Back to Ellipse Lesson
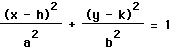 . From this, one will notice that if both h and k
are zero, the equation resembles the standard form of the equation when
the ellipse is centered at the origin. Thus, h and k not only
determine the center of the ellipse but the shift of the ellipse in the
x and y directions also, respectively. The graphs below illustrate
ellipses not centered at the origin but rather at some point (h,k).
. From this, one will notice that if both h and k
are zero, the equation resembles the standard form of the equation when
the ellipse is centered at the origin. Thus, h and k not only
determine the center of the ellipse but the shift of the ellipse in the
x and y directions also, respectively. The graphs below illustrate
ellipses not centered at the origin but rather at some point (h,k).

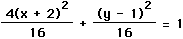
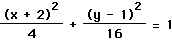
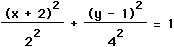
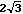 . If this ellipse was centered at the origin, the coordinates
of the vertices of the major and minor axes would be (0,-4), (0,4),
(-2,0) and (2,0), respectively, and of the foci would be
(0,-
. If this ellipse was centered at the origin, the coordinates
of the vertices of the major and minor axes would be (0,-4), (0,4),
(-2,0) and (2,0), respectively, and of the foci would be
(0,-