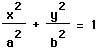. When graphed, this ellipse
looks like one of the two figures belowThe equation of an ellipse in standard form centered at the origin looks
like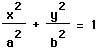. When graphed, this ellipse
looks like one of the two figures below
|
|
An ellipse has two axes of symmetry. The longer axis is called the major axis and the shorter axis is called the minor axis. From the picture of an ellipse above, when a > b, one can see that the major axis is along the line y = 0 and the minor axis is along the line x = 0, and when b > a, one can see that the major axis is along the line x = 0 and the minor axis is along the line y = 0. The foci of the ellipse are determined by the major axis and the equation c2 = a2 - b2 if a > b or c2 = b2 - a2 if b > a. From the definition of an ellipse, one should be able to understand that the focal constant (the sum of the distance from (-c,0) to (x,y) and (c,0) to (x,y)) of an ellipse is equal to the length of the major axis. Also from these pictures, one can see that the endpoints(or vertices) of the major and minor axes are (-a,0), (a,0), (0,-b), and (0,b) and the foci are (-c,0) and (c,0) for a > b, and (0,-c) and (0,c) for b > a.
Now that we know what the standard form for an ellipse is, let us put the equation 9x2 + 25y2 = 225 into standard form, find the vertices and foci for this ellipse, and graph the ellipse.
The first step in changing this equation to standard form is to divide both sides of the equation by 225 because we need a 1 on the right side of the equation. After this division and some simplification we have
=>
=>
Thus, a = 5, b = 3 and c = 4. From this, we find that the vertices are located at (-5,0), (5,0), (0,-3), and (0,3) and the foci are (-4,0) and (4,0). The graph of this ellipse looks like
